El mundo matemático es amplio y, a veces, extremadamente complejo. No obstante, todo en el universo son matemáticas. Y dentro de este universo tan completo y complicado, hoy nos vamos a centrar en los números primos.
Recuerda que un número es un ente abstracto que forma una serie ordenada. Además, cada uno de ellos indica una cantidad de elementos dentro de un conjunto.
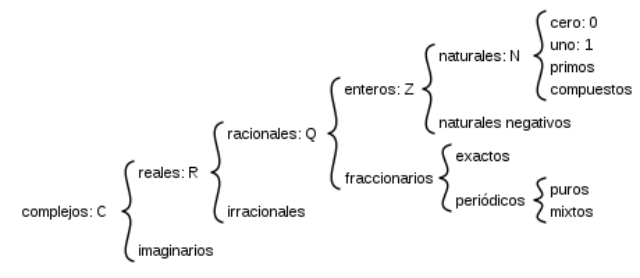
Ahora bien, en el mundo de los números, también encontramos una buena cantidad de tipos de ellos. Por eso, hoy, como hemos comentado, nos centramos en los primos.
Qué son los números primos
Un número primo es un entero positivo que difiere del 0 y, a veces, del 1. Pero su característica más definitoria es que únicamente puede ser dividido por sí mismo y por 1 para que se obtenga una solución exacta.

Para entender bien a qué nos referimos, vamos a verlo en un ejemplo:
- Si tomamos el número 3 y los intentamos dividir entre 2, por ejemplo, el resultado es 1,5, que no es un número entero. Es decir, que para obtener un resultado entero, el 3 solo se puede dividir entre 1, que da 3, y entre 3, que da 1. O sea, el tres es un número primo.
- Si tomamos el 4, por ejemplo, observamos que al dividirlo entre 2, el resultado obtenido es igualmente 2. O sea, que este no es primo, pues el resultado es entero, tiene otros divisores.
Números primos hay muchos, tantos, que probablemente sean infinitos. El 2, el 3, el 5, el 7, el 11, el 13, el 17, el 29… Y así podríamos seguir todo el día.
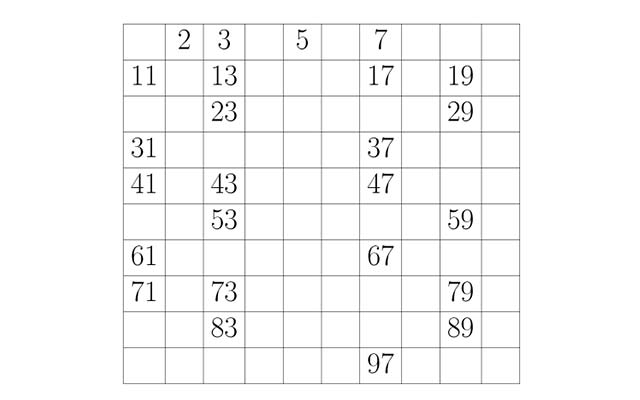
Aun así, existen casos especiales, como es el 1. No todo el mundo lo considera primo. Es cierto que solo tiene un divisor, que es el propio 1, pero depende de cada cultura, su definición varía. Por ejemplo, antiguamente, en Grecia, los números comenzaban en el 2, por lo que este no estaba considerado como tal.
Otra particularidad la encontramos en el 2, que está considerado como el único primo par que existe en el mundo que se sepa.
Otras consideraciones sobre los números primos

Dentro del mundo de los números primos encontramos muchas particularidades, por ejemplo:
- Los números gemelos: son aquellos primos cuya diferencia es 2. Por ejemplo, si restamos 7 – 5, ambos primos, obtenemos un 2, quiere decir que los dos son gemelos.
- Primos de Mersenne: son primos que se expresan como N=(2^n)-1, donde N es el primo de Mersenne y n es cualquier número. Solo se conocen 37.
- Conjetura de Goldbach: propuesta por el matemático del mismo nombre en 1742, considera que cualquier número par superior a 2 se puede expresar como una suma entre dos números primos. Por ejemplo, 6=3 +3, 8=5 + 3, etc. Nadie lo ha podido refutar, por lo que se considera una conjetura cierta, aunque no ha sido comprobada.
Y así llegamos al final. Desde el año 300 a.C., Euclides demostró que los números primos son infinitos. Así sigue, no ha cambiado en más de 23 siglos esta afirmación.

